Analytical Questions: Light
Numerical Questions: Light
Recall
Refractive Index:
The refractive index n of a medium is a dimensionless number that describes how light propagates through that medium. It is defined as the ratio of the speed of light in a vacuum c to the speed of light in the medium v:
n = c/v
n (Refractive Index): It indicates how much the light slows down when it enters the medium. The higher the refractive index, the slower the light travels through the medium.
c: The speed of light in a vacuum, approximately 3×108 m/s
v: The speed of light in the medium.
Refractive indices can vary depending on the nature of the medium and the circumstances under which light is passing through it.
1. Absolute Refractive Index
The absolute refractive index of a medium is the ratio of the speed of light in a vacuum to the speed of light in that medium.
Formula: n = c/v
where c is the speed of light in a vacuum, and v is the speed of light in the medium.
2. Relative Refractive Index
The relative refractive index is the ratio of the speed of light in one medium to the speed of light in another medium. It indicates how light will bend or change direction when transitioning between two different media.
Formula: n₂₁ = v₁/v₂ = n₂/n₁
v1, v2 are the speeds of light in media 1 and 2, respectively, and n1and n2 are the absolute refractive indices of media 1 and 2.
For Spherical Mirrors
1. Concave Mirror
Focal Length (f) is Negative (as Focus is to the left of Pole)
Converging Mirror
Forms Real and Inverted Image. (Except when object is between F and P)
S. No. |
Position of Object |
Position of Image |
Size of Image |
Nature of Image |
1 |
Object at Infinity |
At the Focus |
Highly Diminished |
Real and Inverted |
2 |
Object Beyond the Centre of Curvature |
Between the Centre of Curvature and Focus |
Diminished |
Real and Inverted |
3 |
Object at the Centre of Curvature or Focus |
At the Centre of Curvature |
Same Size |
Real and Inverted |
4 |
Object Between the Centre of Curvature and Focus |
Behind the Centre of Curvature |
Enlarged |
Real and Inverted |
5 |
Object at the Focus |
At Infinity |
Highly Enlarged |
Real and Inverted |
6 |
Object Between the Focus and the Pole |
Behind the Mirror |
Enlarged |
Virtual and Erect |
2. Convex Mirror
Focal Length (f) is Positive (as Focus is to the right of Pole)
Diverging Mirror
Always forms Virtual, Erect & Diminished Image.
Mirror Formula:
1/f = 1/u + 1/v
Magnification m = hi/ho = -v/u
m = 1 –> Object and Image equal in height
m > 1 -> Image is Enlarged
m < 1 -> Image is diminished
m is positive indicates Virtual and Erect Image
m is negative indicates Real and Inverted Image
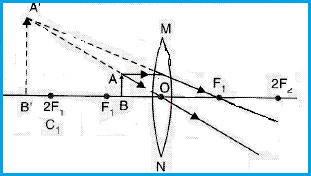
L Lens
1 1. Convex Lens
Focal Length (f) is positive
Converging Lens
Forms Real and Inverted Image except when object is between F1 and O
Power is also positive
Position of the object |
Position of the image |
Relative size of the image |
Nature of the image |
At infinity |
At focus F2 |
Highly diminished |
Real and inverted |
Beyond 2F1 |
Between F2 and 2F2 |
Diminished |
Real and inverted |
At 2F1 |
At 2F2 |
Same size |
Real and inverted |
Between F1 and 2F1 |
Beyond 2F2 |
Enlarged |
Real and inverted |
At focus F1 |
At infinity |
Infinitely large or highly enlarged |
Real and inverted |
Between focus F1 and the optical center O |
On the same side of the lens as the object |
Enlarged |
Virtual and erect |
2. Concave Lens
Focal Length (f) is negative
Diverging Lens
Always forms Virtual, Erect and Diminished Image
Power is also Negative
Lens Formula:
1/f = 1/v - 1/u
Magnification m = hi/ho = v/u
Solved Numerical:
diminished image.
such an image. Because Concave Mirror also formed Erect and Virtual image when object is
between Focus (F) and Pole (P), However it forms an enlarged image.
the mirror.
(ii) Find the distance of the image from the object.
(iii) What is the focal length of the mirror?
Solution:
same size image as that of the object.
(i) The mirror is concave since it forms a real image. The case when an object is at center of
curvature (C), then the same size image is formed at center of curvature (C).
(ii) A magnification of -1 implies that both the object and image are located at the center
of curvature, C. The distance of the image from the object is zero.
(iii) The radius of curvature is 50 cm. So, the focal length is 25 cm (1/2 x radius of
curvature).
(iv) The image formation is shown below.
cm to 15 cm. justify your answer without using mirror formula.
Solution:
If the object is placed at 25 cm in front of the concave mirror having focal length 20 cm, this means that the object is placed in between focus and the center of curvature of the mirror. If the object is placed in front of the center of curvature then the image will be formed beyond the center of curvature. So the image formed is a real image. The nature of the image will be real & inverted and enlarged
If the object is placed at 15 cm in front of the concave mirror having focal length 20 cm, this means that the object is placed in between focus and the pole of the mirror i.e. 10 cm (25 - 15). An object placed between the pole and focus of a concave mirror forms a virtual & erect image. The nature of the image will be will be erect and enlarged.
1. 4. Write one similarity and one dissimilarity between image formed by plane mirror and convex mirror.
Similarity:- Both produce Virtual Image.
Dissimilarity:- Convex Mirror produces diminished image while plane mirror produce the Image of the same size as that of the object.
1. 5. A student has three concave mirrors A, B and C of focal lengths 20 cm, 15 cm and 10 cm
respectively. For each concave mirror he performs the experiment of image formation for three
values of object distance of 30 cm, 10 cm and 20 cm.
Giving reason answer the following:
(a) For the three object distances, identify the mirror which will form an image equal in size to
that of object. Find at least one value of object distance.
(b) Out of the three mirrors, identify the mirror which would be preferred to be used for shaving
purpose.
(c) For the mirror B, draw ray diagram for image formation for any two given values of object
distance.
Given:
fA = 20 cm, fB = 15 cm, fC = 10 cm, u1 = 30 cm, u2 = 10 cm, u3 = 20 cm
a. For same size image, object should be placed at Center of Curvature, ⸪ R = 2 f, i.e. R₁, = 40
cm, R₂ = 30 cm and R₃ = 20 cm from the given focal lengths.
So for Mirror A, Image will not of same size for these positions because no given object
distance is 40 cm.
For Mirror B, Image will be of same size for position u1 = 30cm ⸪ R₂ =30 cm
For mirror C, Image will be of same size for position u3 = 20cm ⸪ R₃ =30 cm
b. We need enlarged and erect image for shaving. For erect and enlarged image, Object
should be placed between Pole and Focus. Face would be generally kept at more than
10 cm distance from the pole, so mirrors A and B are suitable for shaving.
c. The required Ray diagrams are as follows:
So, object distance should be less than 12 cm.
when object is between Focus(F) and Pole (P) of a concave mirror.
(iii) Here u = -6 cm, f = -12 cm
Using Mirror Formula
1/f = 1/v + 1/u
1 /−12 = 1 / v + 1 / −6
v = 12 cm
The image is real and inverted as it is formed in front of the mirror.
is real then find the distance of the object from the mirror.
Size of image = n × size of object
n = Size of image / size of object = magnification
Since the image is real, it must be inverted hence magnification will be negative,
m = -n
Let d is the distance of object then,
m = -v/u
-n = -v / d
or
v = nd
Therefore, the mirror formula:
1 / f = 1/v + 1/u
Becomes,
1/f = 1/n x d + 1/d
or
1/f = 1/d (1/n + 1)
or
1/d = n/ f(n + 1)
Therefore,
d = f (n + 1)/ n
8. The object when placed at a distance of 60 cm from a convex mirror, then the magnification produced is
1/2. Where the object should be placed to obtain a magnification of 1/3?
Solution:
u = -60 cm
m = 1/2
So,
-v/u = 1/2
and
v/60 = 1/2
or
v = 30 cm
Since, the mirror formula is:
1 / v + 1 / u = 1 / f
Therefore,
1 / 30 + 1 / (-60) = 1/f
1/f = (2-1) / 60 = 1 / 60
f = 60 cm
Now for magnification = 1 / 3,
– v / u = 1 / 3
or
v = – u / 3
Using mirror formula
1 / v + 1 / u = 1 / f
1 / (-u/3) + 1/ u = 1/ 60
-3/ u + 1/u = 1/60
-2/ u = 1/60
or
u = -120 cm
The object should be placed at 120 cm in front of mirror to get magnification of 1/3.
9. An object 5 cm in length is held 25 cm away from a converging lens of focal length 10 cm. Draw the ray
diagram and find the position, size and the nature of the image formed.
Solution:
Given:
ho = +5 cm, u = -25 cm and f = +10 cm (Lens converging)
using lens formula
1/f = 1/v – 1/u
1/+10 = 1/v – 1/-25
1/v = 1/10 - 1/25
= 3/50
v = 50/3 = 16.67 cm
Also, Magnification m = hi/ho = v/u
= 50/3/-25
= -2/3
The negative sign indicates that it is a Real and Inverted Image.
Now, m = hi/ho
hi = m x ho
= -2/3 x 5
= -10/3 cm (The height is 10/3 cm or 3.33 cm in front of the mirror.
prescribed lens diverging or converging?
Solution:
Given: P = +1.5 D
f = 1/P = 1/+1.5 = 0.67 m.
As the power of lens is (+ve), the lens is converging lens.
the diagram. If arc AB = 12 arc CD, what is the ratio of their focal lengths? State which of the two mirrors
will always form virtual image of an object placed in front of it and why?
Focal length of a mirror is given by
Focal length = Radius of curvature /2
Since both the mirrors have same radius of curvature, therefore focal length of the two mirrors will be same, i.e.
f1/f2 = 1/1
Since virtual image is always formed by convex mirror. The mirror AB will always form virtual image.
calculate the linear magnification.
Let the Focal length of mirror = f
So, the object distance, u = -2f
The formula to calculate image distance we use mirror formula as,
1 / v + 1 / u = 1 / f
Therefore,
1 / v + 1 / -2f = 1 / f
1 / v = 1 / f + 1 / 2f
= 3 / 2f
or
v = 2f / 3
Magnification is given as,
m = – v / u
= - (2f/3) / (-2f)
= 1/3
13. The image of an object formed by a lens is of magnification -1. If the distance between the
object and its image is 60 cm, what is the focal length of the lens? If the object is moved 20
cm towards the lens, where would the image be formed? State reason and also draw a ray
diagram in support of your answer.
Solution:
Image with magnification -1 means that - Negative sign indicates image is Real & Inverted, and m = 1 indicates the size of object is same as that of the Image.
Therefore, object is at 2F and the image is also at 2F on the other side of the lens.
Therefore, distance between the object and its image is –
4f = 60 cm
=> f = 15 cm
Object distance 2f = 30 cm,
if the object is shifted towards the lens by 20 cm,
the new object distance = 30 cm - 20 cm = 10 cm.
As can be observed, The new object (10 cm) is distance is less than the focal length (15 cm), and the image formed in this case would be virtual, erect and will form on the same side as the object.
14. The refractive indices of glass and water with respect to air are 3/2 and 4/3 respectively. If speed of
light in glass is 2 × 108 m/s, find the speed of light in water.
The refractive index n of a medium is given by:
n = c / v
where:
c is the speed of light in a vacuum (approximately 3×10⁸ m/s),
v is the speed of light in the medium.
Given:
Refractive index of glass, ng = 3/2,
Refractive index of water, nw = 4/3,
Speed of light in glass, vg = 2×108 m/s
We know the refractive index of glass is:
ng = c/vg ----- (1)
Now, to find the speed of light in water vw, we use:
nw = c/vw --------- (2)
from (1) and (2), We have, ng/ nw =
= (c x vw) /(c x vg)
= vw / vg
(3/2) /(4/3)
vw = (9 x 2 x 10⁸) /(8)
= 2.25 x 108 m/s
 Reviewed by Syed Hafiz Choudhary
on
August 27, 2024
Rating:
Reviewed by Syed Hafiz Choudhary
on
August 27, 2024
Rating:











very nice content
ReplyDelete